Large set (Ramsey theory)

For other uses of the term, see Large set (disambiguation).

In Ramsey theory, a set S of natural numbers is considered to be a large set if and only if Van der Waerden's theorem can be generalized to assert the existence of arithmetic progressions with common difference in S. That is, S is large if and only if every finite partition of the natural numbers has a cell containing arbitrarily long arithmetic progressions having common differences in S.

1 Examples
2 Properties
3 2-large and k-large sets
4 See also
5 References
6 External links

Examples

The natural numbers are large. This is precisely the assertion of Van der Waerden's theorem.
The even numbers are large.

Properties

Necessary conditions for largeness include:

If S is large, for any natural number n, S must contain infinitely many multiples of n.
If 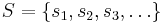$S=\{s_1,s_2,s_3,\dots\}$ is large, it is not the case that s_k≥3s_k-1 for k≥ 2.

Two sufficient conditions are:

If S contains n-cubes for arbitrarily large n, then S is large.
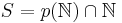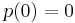If $S =p(\mathbb{N}) \cap \mathbb{N}$ where $p$ is a polynomial with $p(0)=0$ and positive leading coefficient, then $S$ is large.

The first sufficient condition implies that if S is a thick set, then S is large.

Other facts about large sets include:

If S is large and F is finite, then S – F is large.
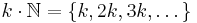$k\cdot \mathbb{N}=\{k,2k,3k,\dots\}$ is large. Similarly, if S is large, 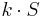$k\cdot S$ is also large.

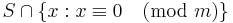If $S$ is large, then for any $m$ , $S \cap \{ x�: x \equiv 0\pmod{m} \}$ is large.

2-large and k-large sets

A set is k-large, for a natural number k > 0, when it meets the conditions for largeness when the restatement of van der Waerden's theorem is concerned only with k-colorings. Every set is either large or k-large for some maximal k. This follows from two important, albeit trivially true, facts:

k-largeness implies (k-1)-largeness for k>1
k-largeness for all k implies largeness.

It is unknown whether there are 2-large sets that are not also large sets. Brown, Graham, and Landman (1999) conjecture that no such set exists.

References

Brown, Tom, Ronald Graham, & Bruce Landman. On the Set of Common Differences in van der Waerden's Theorem on Arithmetic Progressions. Canadian Math Bulletin, Vol 42 (1), 1999. p 25-36. pdf

External links

Mathworld: van der Waerden's Theorem